Fractions Misconceptions and Thinking-in-Change: Samuel and the Equivalent Fractions
Misconceptions are a bi-product of children developing their own connections as they experience mathematics in school and in the world around them (Hansen, 2012, 2014).
In the iTalk2Learn project we are designing tasks and task-dependent support for the exploratory learning environment, Fractions Lab (see WP3 news report for more on Fractions Lab), to explicitly highlight students’ misconceptions that will allow us to capitalise upon their misunderstandings to support conceptual understanding.
Below is a case study from a recent study where one child, who we will call Samuel, was using Fractions Lab to make equivalent fractions. Samuel is 10 years old and is of average attainment in maths. In this case study he exhibits the misconception ‘x/y = 1/x.y’ which has also been observed in other task trials with other children, so it appears to be a fairly common misconception held by students in the age range we are working with (9-11 years).
In the case study we look at Samuel’s thinking-in-change in order to observe how the task sets his thinking in motion, see how his ideas are in turbulence and then how new notions are connected to what he already knows (Noss & Hoyles, 1996:9-10).
Samuel’s misconception
Samuel announces that 2/6 = 1/12 because ‘two sixes equals twelve’ and he proceeds to construct the two fractions on the screen to demonstrate this fact. Immediate feedback from the ‘equivalence tool’ informs Samuel that the two fractions are not equivalent (see figure 1). He expresses surprise and states ‘this [computer] is wrong’. When asked why, he responds: ‘The computer is wrong because I know that 1/12 equals 2/6’.
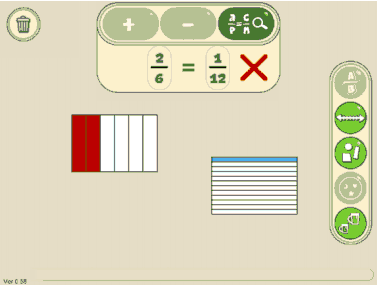
Fig. 1: Samuel uses the equivalence tool to show 2/6 = 1/12, then states the computer is “wrong”
In fact the misconception is so strongly held by Samuel that he goes on to try out 2/4 and 1/8 to test the computer because he ‘knows’ that 2/4 = 1/8 (because 2 x 4 = 1 x 8) (see Figure 2).
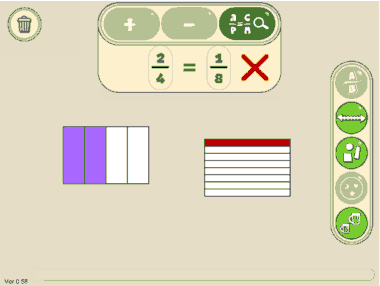
Fig. 2: Samuel uses the equivalence tool to show 2/4 = 1/8
Observing Samuel’s ‘thinking-in-change’
Seeing this feedback from Fractions Lab encourages Samuel to challenge his assumptions (‘I know one twelfth equals two sixths [pause] or is it I’m wrong? I don’t know… I don’t know which one it is.’). After a short period of trial and error, Samuel finds that he receives a green tick when he enters 2/4 and 4/8 into the equivalence tool (‘Yay! It worked!’). Upon prompting, Samuel does not see an alternative mathematical relationship between the fractions, but instead believes that he did not use the computer correctly (‘Oh! I needed to tell the computer what I was doing. Tell it that I’m making one twelfth equals two sixths.’) So this initially appears to be a dead-end.
However, without prompting Samuel says ‘I know what I did wrong… need to have one twelfth equals twelve [pause] fourths, no, no, no I’m confused.’ So we begin to witness some turbulence in Samuel’s thinking which has challenged his existing connections and he is trying to articulate an alternative. He continues to explore why 2/4 and 4/8 ‘works’ by asking himself the question, ‘so what makes this one work that the other one doesn’t?’
After a period of silence Samuel says, ‘two 4s equals four 8s. What’s four 8s? 32. So I need to make a thirty two[th].’ This line of thinking is not continued and after a period of talking about children outside the classroom, Samuel is encouraged by the researcher to try out 2/6 and 1/12 and to find two fractions that are equivalent. After making 2/6 again, Samuel first partitions 1/12 so it becomes 2/24 then divides the rectangle further into 26ths before making a numerator of 4 and appears to instruct the numerator to ‘wait there’.
Then he changes the number of sections the rectangle is split up into (up to 30 and then reduces the number) until he gets to 10. He says, ‘wait’, makes a denominator of 12 then 14 and announces, ‘wait, is it 12? Let’s try that one’ (see figure 3). He is joyful when he sees that it is correct.
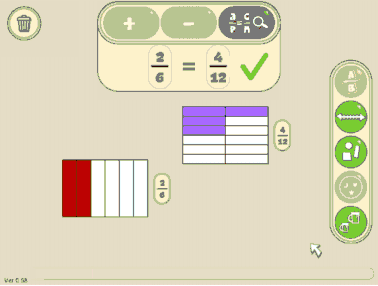
Fig. 3: Samuel has received feedback that 2/6 = 4/10. Earlier he selected to be able to see the fraction symbol next to each fraction permanently
When prompted by the researcher to explain why, Samuel says, ‘What is four twelves? Forty eight. [Pause] I know what I did. It’s got to make up the same number. So they’re a bit the same. They are in the same times table. One’s 4 and one’s 2, so 2 add 2 equals 4 and then 6 add 6 is 12.’
Discussion: How Fractions Lab appears to help students address their misconceptions
The episode described above is 12:45 minutes long. In that relatively short time period, we have witnessed Samuel’s thinking-in-change about the ‘x/y = 1/x.y’ misconception he holds strongly. The task set Samuel’s thinking in motion by asking him to make four equivalent fractions. This is an open-ended task and therefore enabled Samuel to use fractions of his choice.
Because Fractions Lab is an exploratory learning environment, in tasks such as the one in this case study, students are allowed to select the representation they choose. In this particular case study, Samuel used one vertical rectangle (so called because it splits vertically) and one horizontal rectangle (so called because it splits horizontally, although in this case Samuel also partitioned it in two).
We can argue that if Samuel had been prompted to select the same representation so that he could compare like-with-like, then he may have come to a conclusion earlier. We can only guess whether or not Samuel would have focused to the same level on the symbols themselves.


